C# 8 using declarations

Visual Studio 2019 preview 2 was released a few days ago and I took the time to install it. Visual Studio itself is actually rather uninteresting to me, however the inclusion of the next C# 8 preview got my attention. I glanced at the feature highlights and posted “looks nice” on Twitter.

Predictably, I got a few responses like “I’m not sure I like that”, and there is always a guarantee that if F# has a similar feature, an F# developer will appear and tell you F# has had this feature for 600 years.

The one I like a lot is using declarations. This allows a local to automatically be disposed at the end of the block. Essentially, it hides the try/finally or the using() {...}. The .NET team’s blog kind of gave a bad example of this, so I’ll use one from Open OPC SignTool. Here is the original snippet:

private static X509Certificate2 GetCertificateFromCertificateStore(string sha1)
{
    using (var store = new X509Store(StoreName.My, StoreLocation.LocalMachine))
    {
        store.Open(OpenFlags.OpenExistingOnly | OpenFlags.ReadOnly);
        var certificates = store.Certificates.Find(X509FindType.FindByThumbprint, sha1, false);
        return certificates.Count > 0 ? certificates[0] : null;
    }
}

A using var can make this:

private static X509Certificate2 GetCertificateFromCertificateStore(string sha1)
{
    using var store = new X509Store(StoreName.My, StoreLocation.LocalMachine);
    store.Open(OpenFlags.OpenExistingOnly | OpenFlags.ReadOnly);
    var certificates = store.Certificates.Find(X509FindType.FindByThumbprint, sha1, false);
    return certificates.Count > 0 ? certificates[0] : null;
}

This has the same effect of store having Dispose called on it at the end of the method. The benefit here being that there is less indentation and braces. This keeps me focused on the code that matters. I don’t care when store is disposed in the method, I can just observe that it has a using modifier on the local and be assured that Dispose will be called.

This isn’t the same as garbage collection or finalizers. Both of those are non- deterministic, and can lead to unexpected program behavior. That’s less so in the case of X509Store, so let’s look at another example:

using Stream stream = entry.Open();
var xmlDocument = XDocument.Load(stream, LoadOptions.PreserveWhitespace);
return new OpcRelationships(location, xmlDocument, readOnlyMode);

Not disposing a stream that is backed by a file can cause access errors later in software that might try to open that file again - it is already open, so not only is it a bad idea it leave streams to the GC, it is just simply incorrect.

However again using on the local ensures it is deterministically closed.

When it gets disposed I can see being slightly unclear to the developer. The quick explanation is when the local is no longer reachable, not when it is last used. The C# 8 above gets compiled roughly to:

var stream = entry.Open();
try
{
    var xmlDocument = XDocument.Load(stream, LoadOptions.PreserveWhitespace);
    return new OpcRelationships(location, xmlDocument, readOnlyMode);
}
finally
{
    if (stream != null)
    {
        ((IDisposable)stream).Dispose();
    }
}

The disposal is done after the return, when the local is no longer reachable, not after XDocument is created.

I find this very helpful to keep code readable. This doesn’t work when you need fine control over when Dispose is called. A place where this does not work well is when the Dispose pattern is used for scopes, such as logging. The AzureSignTool project has code similar to this in SignCommand:

var logger = loggerFactory.CreateLogger<SignCommand>();
Parallel.ForEach(AllFiles, options, () => (succeeded: 0, failed: 0), (filePath, pls, state) =>
{
    using (var loopScope = logger.BeginScope("File: {Id}", filePath))
    {
        logger.LogInformation("Signing file.");
        //Sign the file. omit a bunch of other code.
        logger.LogInformation("Done signing the file.");
    }
    logger.LogDebug("Incrementing success count.");
    return (state.succeeded + 1, state.failed);
}

Here, we cannot change this to a using var because then the LogDebug would be inside of that logging scope, which it wasn’t before. This is a place where we continue to want Dispose to be called at a different time from the when loopScope would no longer be in scope.

My impression from C# developers is that they do not tend to call Dispose on resources as soon as it can be disposed, just at a reasonable point in the same method. Most developers do not write this code:

public bool MightBeExe(string filePath)
{
    var firstBytes = new byte[2];
    int bytesRead;
    using (var file = File.Open(filePath, FileMode.Open))
    {
        bytesRead = file.Read(firstBytes, 0, 2);
    }
    return bytesRead == 2 && firstBytes[0] == (byte)'M' && firstBytes[1] == (byte)'Z';
}

They will instead write something like:

public bool MightBeExe(string filePath)
{
    using (var file = File.Open(filePath, FileMode.Open))
    {
        var firstBytes = new byte[2];
        var bytesRead = file.Read(firstBytes, 0, 2);
        return bytesRead == 2 && firstBytes[0] == (byte)'M' && firstBytes[1] == (byte)'Z';
    }
}

Which is a perfect candidate for using var:

public bool MightBeExe(string filePath)
{
    using var file = File.Open(filePath, FileMode.Open);
    var firstBytes = new byte[2];
    var bytesRead = file.Read(firstBytes, 0, 2);
    return bytesRead == 2 && firstBytes[0] == (byte)'M' && firstBytes[1] == (byte)'Z';
}

There are of course some reasonable limitations to this feature. For example, it cannot be combined with out-variables.

if (Crypto32.CryptEncodeObjectEx(
    // other stuff
    out var handle,
    ref size)
)
{
    using (handle)
    {
        // Do stuff
    }
}

This does not work:

if (Crypto32.CryptEncodeObjectEx(
    // other stuff
    out using var handle,
    ref size)
)
{
    // Do stuff
}

Jared Parsons said on Twitter that C# folks thought of this, and decided that it had “Too much confusion about ownership.” Thinking about it myself, I agree, so it’s nice that the feature is limited in that regard.

Another limitation is that the variable cannot be reassigned. For example:

using var stream = entry.Open();
stream = entry2.Open();

This will produce error CS1656, “Cannot assign to ‘stream’ because it is a ‘using variable’”.

All in all, I very much like this small feature in C# 8. It has reasonable guard rails on it from doing something too weird like re-assigning to it, while giving the benefit of less blocks, braces, indentation.

Secure Random Integers in .NET Core 3

.NET Core 3.0 is tentatively set to include a new API for securely generating a random integer bound to a specific range.

I won’t be shy in admitting that it was something I pushed for and made the initial attempt at implementing, though it’s unfair to say that I implemented it by myself given all of the outstanding feedback I got on the initial pull request (thanks Levi and Jeremy!)

It’s been known for a while that System.Random shouldn’t be used when cryptographic randomness is required. Despite that, there wasn’t anything built in to .NET that made creating bounded random integers easy. You could either use System.Random and hope for the best, or use a CSPRNG like RandomNumberGenerator that gave back raw bytes, which requires some thought on how to to properly convert it to a random integer without introducing any kind of bias.

Starting in .NET Core 3.0, you’ll be able to do:

var min = 1;
var max = 1_000;
var randomNumber = RandomNumberGenerator.GetInt32(min, max);

If you need this before .NET Core 3, well, the source is right there. It can be adapted with a bit of effort to work on the .NET Framework as well as other environments that don’t have Span<T>.

FixedTimeEquals in .NET Core

.NET Core introduced FixedTimeEquals which I have personally found to be very helpful. It’s a small method, but given the kind of code I tend to write, I was writing it a lot from project to project, and am happy to see it in the box.

This API is meant to prevent a timing side-channel when comparing two sequences of bytes. The goal is, the comparison should take the same amount of time regardless of the contents of the bytes, assuming they are the same length. This is often required when doing comparisons of MACs or simple possession demonstrations for APIs.

Consider you had a web API that required an API key and was implemented in such a way that it just expected a magic string to act as a password to interact with the API.

It required an HTTP header, like

X-Api-Key: SecretVooDooWord

and TLS was used to ensure it was kept confidential in transit. The API did a naive implementation like this:

[HttpGet]
public IActionResult SuperSensitiveApi() {
    var key = Request.Headers["X-Api-Key"].Single();
    if (key != "SecretVooDooWord") {
        return Unauthorized();
    }
    return new JsonResult(new { AllTheSecretData = "tada" });
}

The issue here is that neither != or == are fixed-time, and will return false as soon as there is an immediate difference. In pseudo code, it might look something like this:

compare(word1, word2) {
    if word1.length != word2.length
        return false
    i = 0
    while (i < word1.length) {
        letter1 = word1[i]
        letter2 = word2[i]
        if letter1 != letter2
            return false
        else
            i = i + 1
    }
    return true
}

This function will compare the letters one by one. As soon as it encounters a difference, it returns false and doesn’t bother checking the rest. Why should it? The answer is going to be false every time.

To an attacker that is trying to figure out the contents of the string, carefully measuring the time can leak the contents of the string. For argument’s sake, let’s say that checking each letter takes 2ns and the attacker has a very accurate way of measuring time over a network and can account for jitter and latency.

GET /SuperSensitiveApi HTTP/1.1
X-Api-Key: Raaaaaaaaaaaaaaa

Checking the API key will take 2ns because the first letters do not match. The attacker moves on to the next letter.

GET /SuperSensitiveApi HTTP/1.1
X-Api-Key: Saaaaaaaaaaaaaaa

This time, checking the API key takes 4ns because the first letter matched (2ns) and the second failed (another 2ns)

GET /SuperSensitiveApi HTTP/1.1
X-Api-Key: Sbaaaaaaaaaaaaaa

Fails again taking 4ns to check the API key. After a few more tries…

GET /SuperSensitiveApi HTTP/1.1
X-Api-Key: Seaaaaaaaaaaaaaa

This time it took 6ns to check the API key because the first and second letter were checked, and the third failed.

The attacker can keep doing this by observing the amount of time each call takes. The longer it takes, the attacker can assume they have guessed the next letter. In practice, this is extremely difficult to do over a network and to get accurate enough timing information, but it is believed that it might be possible given enough persistence and an adversary that has the means to be in a network position that is very stable.

These kinds of attacks do exist, an example timing side-channel is Lucky 13, which affected many library’s approach to handling CBC padding in TLS.

So == in C# is a bad way to check strings for equality where timing side channels need to be mitigated. So you say, perhaps you’ll do something like this:

private static bool CheckStringsFixedTime(string str1, string str2) {
    if (str1.Length != str2.Length) {
        return false;
    }
    var allTheSame = true;
    for (var i = 0; i < str1.Length; i++) {
        if (str1[i] != str2[i]) {
            allTheSame = false;
        }
    }
    return allTheSame;
}

This looks like it’s constant time, but on modern CPUs and .NET, it’s not. Branch statements, like if, have timing implications. We can’t take a branch.

OK, what about this?

private static bool CheckStringsFixedTime(string str1, string str2) {
    if (str1.Length != str2.Length) {
        return false;
    }
    var allTheSame = true;
    for (var i = 0; i < str1.Length; i++) {
        allTheSame &= str1[i] == str2[i];
    }
    return allTheSame;
}

This looks somewhat promising for C#. We know from the language specification that &= does not short circuit, so str1[i] == str2[i] will always be evaluated.

We still have a few problems though, and this is where the JIT and x86 can make things more complicated for us.

The first issue is that allTheSame is a simple true/false flag. That still leaves the .NET JIT and x86 instruction execution to make a few optimizations that introduce timing attacks. Timing side channel mitigation should avoid all decisions until the very end. & is a decision. However, we can improve that some:

private static bool CheckStringsFixedTime(string str1, string str2) {
    if (str1.Length != str2.Length) {
        return false;
    }
    var result = 0;
    for (var i = 0; i < str1.Length; i++) {
        result |= str1[i] ^ str2[i];
    }
    return result == 0;
}

This is fairly close to being time-fixed. We update an integer using | to combine the bits from the result of an XOR. XOR anything with itself, and the the result is zero. Anything else, and you get a non-zero value. We use a binary OR to combine any bits. At the end, if we have a non-zero value, we know one of the comparison checks failed.

There is some debate as to what arithmetic operators are better for fixed time operations between str1[x] and str2[x]. Some implementations use XOR, like above, other may use SUB for subtraction. Unfortunately, most CPU architectures make no guarantee if any operations are constant-time.

We still have a problem to address. The JIT could be making unintended optimizations. The C# compiler itself makes very little optimizations. The JIT on the other hand may do all sorts of things, like unroll a loop or make a variety of optimizations so the code executes faster.

We can tell the JIT to leave it alone, like so.

[MethodImpl(MethodImplOptions.NoInlining | MethodImplOptions.NoOptimization)]
private static bool CheckStringsFixedTime(string str1, string str2) {
    if (str1.Length != str2.Length) {
        return false;
    }
    var result = 0;
    for (var i = 0; i < str1.Length; i++) {
        result |= str1[i] ^ str2[i];
    }
    return result == 0;
}

So now the JIT will cease to optimize this method at all and it will be closer to as-written.

This is close to time-independent as possible with the String type. We can improve things a bit by making the parameters ReadOnlySpan<char> which will generate very similar x86 as string parameters, however the null checks will be eliminated since a ROS cannot be null.

This is what .NET Core 2.1’s FixedTimeEquals does. It just does it over a ReadOnlySpan<byte> instead of characters. The x86 produced by the current JIT will be identical for ReadOnlySpan<char> and ReadOnlySpan<byte> with the exception of the size of the MOVZX.

It’s handy that this is just in the box for .NET Core now.

Playing with RISC-V

Over the past few years I’ve started to sour on x86 architecture for just about everything. From servers, desktop, and mobile, I’ve long wished we had architectures competing with x86 at the high end.

Fortunately, there are plenty of architectures out there. From ARM and ARM64, to MIPS, there are choices. There is one recent one that has been getting my attention lately, and I’ve thought it’s time to start diving in to it.

RISC-V

RISC-V (pronounced “Risk Five”) is a fairly new architecture that has some interesting ideas behind it that make it worth looking it. Originally designed at UC Berkeley, it is an open architecture with the goal of being applicable to a wide range of devices.

An open ISA that is available for commercial use is not unique, but it is rare. Contrast to ARM, if you want to make your own ARM CPU, you need to license the ISA from ARM Holdings Group, to the tune of millions of dollars. While “open” is not a direct benefit to developers, it does mean that a variety of companies that fabricate their own silicon are interested.

RISC-V is also designed for multiple device profiles. It supports 32-bit and 64-bit, and is broken down in to a set of extension instruction sets, plus the always available integer base set. The ISA also documents and reserves a 128-bit architecture.

This “base” integer instruction set is present on any RISC-V implementation. Often called “RV32I” for 32-bit, or “RV64I”, this instruction set consists of 47 instructions required to move memory, perform computations, and arithmetic.

As of writing, some of the designs of the RISC-V architecture are still under active development, while others are finalized. The RV64I and RV32I are complete, while RV128I is still open for changes. The RV64I and RV32I set guarantees 32 registers. For smaller implementations, there is RV32E which limits the register count to 16.

The extensions are are follows

• “M” extension instructions offer multiplication and division.
• “A” extension instructions offer atomic instructions.
• “C” extension instructions are a few compressed for smaller encoding.
• “F” extension instructions offer single-precision floating point.
• “D” extension instructions offer double-precision floating point.
• “Q” extension instructions offer quad-precision floating point.
• “L” extension instructions offer decimal floating point.

There are more than that, but these are the basic and complete extensions. A vendor may choose to implement any, or none, of these extensions. Most of these extensions can be emulated with the base Integer instructions using compiler replacements, save for the atomic instruction set.

A key aspect though is that the ISA leaves open guidance and design for allowing a vendor to implement their own extensions and describing how they would be encoded.

The extension set is not entirely meant to be pick and choose whatever. The RV32E base set was designed with only supporting the M, A, C extensions in mind, plus any additional extensions sets implemented on top of it.

Hardware

That all sounds swell. But what about actual hardware? Currently, there is not a lot of hardware out there. SiFive though, makes a board called the HiFive 1 which is a small board with an RV32IMAC capable processor.

Notably, it works with the Arduino Studio, so there is a plenty easy way to get started with that.

I however didn’t have a lot of interest in using it as a board to run code that I already knew, I wanted to learn the instruction set, which meant I wanted to write assembly and throw it at the board and see what it did.

I initially struggled doing this in WSL for some reason, the details of which I haven’t quite fully comprehended yet. After switching to MacOS, things went a lot smoother, since much of the documentation was for Linux and Unix-like systems.

I decided to start with a very simple program. Add two numbers.

.section .text
.globl _start
_start:
    li t1, 42
    li t2, 48
    add t3, t1, t2
    nop

li is “load immediate” which allows putting numbers in to registers immediately. The t prefixed registers are temporary registers. A simple compile might look something like this:

riscv32-unknown-elf-gcc example.S -nostdlib -o example.elf

This will produce a binary that is close to working but has a problem that took me a while to track down. The disassembly looks like this:

example.elf:     file format elf32-littleriscv


Disassembly of section .text:

00010054 <_start>:
   10054:	02a00313          	li	t1,42
   10058:	03000393          	li	t2,48
   1005c:	00730e33          	add	t3,t1,t2
   10060:	0001                	nop

Loading this on the HiFive 1 doesn’t work because it doesn’t load at the correct address. Reading through the HiFive 1 ISA and their documentation, the entry point must be at the address 0x20400000. Fortunately, the HiFive 1 comes with a GCC linker script that does all the right things. It handles the start address as well as other memory layout concerns. After re-compiling with their linker script:

riscv32-unknown-elf-gcc example.S -nostdlib -o example.elf -T link.lds

Re-dumping the assembly shows that _start appears in the correct location. Loading the program can be done with openocd, which is included in the HiFive software kit.

Starting it with the correct configuration:

openocd -f ~/.openocd/config/hifive1.cfg 

I moved some files around to make things easier, but they should be easy enough to track down in their software kit.

Once openocd, I can use the included RISC-V GDB debugger to remotely debug it. openocd will start a GDB server on localhost:3333. Firing up the RISC-V GDB, like riscv32-unknown-elf-gdb ~/Projects/riscv/example.elf, I can run the following commands to load the software and start debugging it.

target extended-remote localhost:3333
monitor reset halt
monitor flash protect 0 64 last off
load
layout asm

and if all goes well, we get something like this:

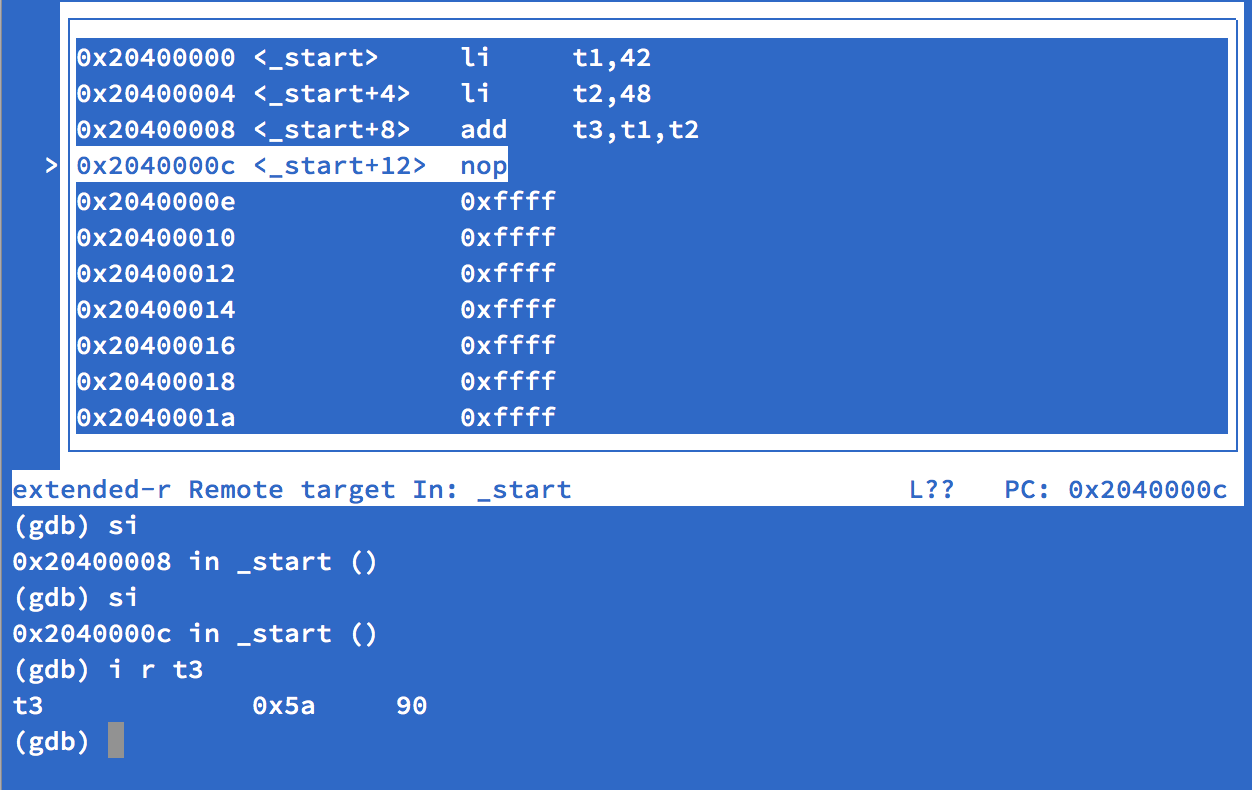
Which is fairly exciting! Debugging my first RISC-V process, even if it does something simple like addition. Performing a few stepi to step a few instructions up to the nop, I can then use info register t3 (or just i r t3 for short) we see we have 90 in the register, which the result of adding 42 and 48.

I’m hopeful that RISC-V will be competitive in the embedded and mobile CPU ISA space. It will take a very long time to get there, and even longer for less homogeneous environment like desktops and laptops, but I believe everyone will be better off if we simply had more to choose from. Even those that will firmly continue to use x86 would benefit from additional innovation and research into architecture design.

I’ll continue to play with RISC-V. If something interesting pops up, I’ll do my best to write about it.

Authenticated Encryption

There’s been some buzz lately about authenticated encryption. The buzz comes from some interesting issues in OpenGPG, and more recently the folks at Microsoft put out an advisory stating that unauthenticated encryption is simply not advisable anymore.

I thought it would be fun to write about cryptography, despite rarely doing it, even though I find it part of what defines me as an engineer and developer.

When we think of “encryption”, we usually think of an entity that has sensitive information they want to protect with a “key” of some kind.

ciphertext = encrypt(plaintext, key)

Something like that. “Decryption” is usually visualized as the process in reverse. The entity has encrypted data that they want to decrypt into its plaintext form because they know the key.

The truth is, well designed systems that rely on cryptography aren’t this simple for a variety of reasons. Further on top of that, software developers struggle to encrypt and decrypt information correctly because many frameworks or libraries that developers depend on offer primitives.

A primitive is a cryptographic function that does very little, but it does its job and it does its job well. That doesn’t mean though that the primitive is enough to fully complete the task. “AES” is a widely known primitive encryption function.

Its most common mode of operation is Cipher Block Chaining, or CBC, which is not authenticated. To put another way, it is malleable. Let’s demonstrate with some ruby code.

require 'openssl'

encrypt_me = "what a fine day for coding" # Data to encrypt
aes_key = (1..16).to_a.pack("C*") # Dummy bad key
aes_iv = (17..32).to_a.pack("C*") # Dummy bad initialization vector
cipher = OpenSSL::Cipher::AES.new(128, :CBC)
cipher.encrypt # Put it in "encrypt" mode, doesn't actually encrypt
cipher.key = aes_key
cipher.iv = aes_iv
ciphertext = cipher.update(encrypt_me) + cipher.final
puts ciphertext.bytes.inspect

Which produces

[15, 90, 144, 183, 105, 160, 17, 219, 160, 166, 20, 201, 53, 30, 2, 29,
217, 115, 3, 249, 2, 170, 203, 32, 37, 234, 147, 188, 167, 254, 254, 192]

There are some bad things in the code example above - it uses a hard-coded, easy to guess key and initialization vector. If you borrow this code, please be wary that it is to demonstrate.

Decryption is a similar process.

aes_key = (1..16).to_a.pack("C*") # Dummy bad key
aes_iv = (17..32).to_a.pack("C*") # Dummy bad initialization vector
cipher = OpenSSL::Cipher::AES.new(128, :CBC)
cipher.decrypt # Put it in "decrypt" mode, doesn't actually decrypt
cipher.key = aes_key
cipher.iv = aes_iv
plaintext = cipher.update(ciphertext) + cipher.final
puts plaintext

Which produces the original string, “what a fine day for coding”.

What if we just… changed the first byte of the cipher text though?

ciphertext[0] = "\1"
# same decryption code as above

That decrypts to “,=m1aH-q8hor coding”. The decryption process didn’t fail in any clear way, it just produced some garbage. We’ve broken the entire “block” of data that we changed a byte in, plus the Nth byte of the next block which was changed. Since we changed the first (0th) byte, the first byte in the second block is “h”, not “f”.

If we slice the data:

plaintext[0..15]  # produces ,=m1aH-q8
plaintext[16..-1] # produces hor coding

If we change the second value of the cipher text:

ciphertext[1] = "\1"

# Decrypt...
plaintext[0..15]  # produces non-ASCII characters
plaintext[16..-1] # produces f4r coding

We see that the “f” is correct for the first byte, but wrong for the second byte.

This is malleable encryption. It allows an attacker to change bits or whole bytes. However the decryption process doesn’t “know” that it is producing invalid data. It’s obvious when you are processing something like text, but it can be less obvious if the data being encrypted is binary data, like a JPEG image.

More interestingly, let’s try changing the last byte of the cipher text:

ciphertext[-1] = "\1"

# Decrypt...

Boom! We get an error, in 'final': bad decrypt (OpenSSL::Cipher::CipherError). Why is that? What we just changed was a padding byte. You might have noticed that when we encrypted our string, the resulting cipher text was bigger than then plain text.

That’s because AES-CBC is a block cipher. It has to operate on chunks of data that are 16 bytes in size. Many implementations will pad the data for you. So when we encrypted “what a fine day for coding”, what actually got encrypted was “what a fine day for coding\6\6\6\6\6\6”.

Where did those \6 bytes come from? That how many bytes it took to reach a multiple of 16. During decryption, it looks at the last byte to determine how much padding to remove.

We can demonstrate this by telling the AES cipher during decryption that there is no padding.

cipher.padding = 0
# Continue decryption...

puts plaintext.bytes.inspect

Which produces:

[119, 104, 97, 116, 32, 97, 32, 102, 105, 110, 101, 32, 100, 97, 121,
32, 102, 111, 114, 32, 99, 111, 100, 105, 110, 103, 6, 6, 6, 6, 6, 6]

So we can see the padding is left there. Six bytes of padding.

Most implementations of AES will automatically apply and remove padding for you.

A poor implementation of AES padding removal will look at the last byte and blindly remove that many bytes:

# Bad padding removal
last_octet = plaintext[-1].ord
unpadded = plaintext[0...-last_octet]

A better implementation of AES padding removal will check that all of the padding bytes are equal to the amount of padding removed.

# Better
last_octet = plaintext[-1].ord
padding = plaintext[-last_octet..-1]
is_padding_valid = padding.bytes.all? { |b| b == last_octet }

# Handle "false" for is_padding_valid
unpadded = plaintext[0...-last_octet]

An even better implementation of AES padding removal would validate the padding in constant time, which is out of my hands with ruby.

It turns out that “false” case for is_padding_valid has caused a lot of problems with AES-CBC, resulting in a padding oracle.

For fun, let’s change the last byte of the first block, and look at the decrypted result and leave the padding on. Remember as we saw previously, changing the Nth byte of the previous block affects the Nth byte of the current block. That’s true for padding as well, it get encrypted like any other data.

ciphertext[15] = "\1"
cipher.padding = 0

#Decrypt...

We get:

[... 110, 103, 6, 6, 6, 6, 6, 26]

Clearly this padding is invalid, because the padding bytes are not all equal to 26. In our home-grown padding removal, is_padding_valid would be false and an error would be returned.

There is one other value that is valid padding, which is 1. If we can change the last byte of the first block so that the last padding byte is one, the padding will appear valid and no error is raised. Let’s use our bad padding removal code and throw an exception if the padding is bad.

def decrypt(data)
    aes_key = (1..16).to_a.pack("C*") # Dummy bad key
    aes_iv = (17..32).to_a.pack("C*") # Dummy bad initialization vector
    cipher = OpenSSL::Cipher::AES.new(128, :CBC)
    cipher.padding = 0
    cipher.decrypt # Put it in "decrypt" mode, doesn't actually decrypt
    cipher.key = aes_key
    cipher.iv = aes_iv
    plaintext = cipher.update(data)
    last_octet = plaintext[-1].ord
    padding = plaintext[-last_octet..-1]
    is_padding_valid = padding.bytes.all? { |b| b == last_octet }
    raise "BAD PADDING" unless is_padding_valid
    return plaintext[0...-last_octet]
end

Our test string is made up of two blocks. We happen to know the padding length is 6, but let’s pretend we don’t. Here is the cipher text. Let’s try and break the last block.

Block 1: [15, 90, 144, 183, 105, 160, 17, 219, 160, 166, 20, 201, 53, 30, 2, 29]
Block 2: [217, 115, 3, 249, 2, 170, 203, 32, 37, 234, 147, 188, 167, 254, 254, 192]

Let’s assume we have a server that we can submit a cipher text to and we have some encrypted data we want to decrypt. The server can accept encrypted data, but it never actually reveals what the plaintext is. The server will either give a padding error back, or say “OK, I was able to decrypt and process the data”.

Remember earlier we said:

We’ve broken the entire “block” of data that we changed a byte in, plus the Nth byte of the next block which was changed.

It goes to reason then, that if we change the last value of the first block, it will affect the last byte of the second block. We are assuming that this encrypted data has padding, but we don’t know how much. Perhaps we can fiddle with the last byte of the penultimate block.

Fortunately, our decryption process makes a nice big fat error when the padding is wrong. The byte of the padding has one or two possible values. The value it is supposed to be (remember, it’s six because we are cheating for now) and one. If it’s one, the padding remover will just remove the last byte. If we just try all combinations for the last byte of the first block, perhaps we can figure out what value makes a padding value of one.

                                                                   Change this
                                                                             ↓
Block 1: [15, 90, 144, 183, 105, 160, 17, 219, 160, 166, 20, 201, 53, 30, 2, 29]
Block 2: [217, 115, 3, 249, 2, 170, 203, 32, 37, 234, 147, 188, 167, 254, 254, 192]
                                                                               ↑
                                                                  To affect this

Let’s loop over it.

(0..255).each do |b|
    # Set last byte of first block
    ciphertext[15] = b.chr
    begin
        decrypt(ciphertext)
        puts b
    rescue
        # The decryption process an error. Skip it and move on.
        next
    end
end

We get two values back. We get 29 and 26. We already know that the value 29 is valid because that’s the actual value from the ciphertext. So 26 forces the padding to one.

Let’s cheat for a moment and verify our findings so that we are comfortable. Given:

ciphertext[15] = 26.chr
decrypt(ciphertext)
return

and if we peek inside the decrypted result with the padding left on, we get:

[95, 9, 61, 149, 138, 173, 150, 56, 255, 200, 46, 73, 45, 145, 185,
77, 102, 111, 114, 32, 99, 111, 100, 105, 110, 103, 6, 6, 6, 6, 6, 1]

The first block is garbage, but crucially we see that we indeed coerce the padding byte to 1.

OK, no more pretending. We know that if we tweak the cipher text’s 15th byte to 26, we end up with a padding of one. What can we learn from that? Let’s take the original ciphertext value, 29, and xor it with our guessed value 26, and then with 1 which is the plaintext value we know it happens to be because the padding was removed successfully.

29 ^ 26 ^ 1 => 6

We were able to figure out the plaintext last byte of the second block. This isn’t “sensitive”, yet, this is the only a padding value. However, we did successfully decrypt a byte without explicit knowledge of the key or the decryption process telling it was 6.

Let’s see if we can figure out how to get the padding to (2, 2).

We can control the last byte of the plaintext now. We can force it to 2 using

ciphertext_value xor known_plaintext_value xor 2

original_ct = ciphertext.dup
ciphertext[15] = (original_ct[15].ord ^ 6 ^ 2).chr
(0..255).each do |b|
    ciphertext[14] = b.chr
    begin
        decrypt(ciphertext)
        puts b
    rescue
        next
    end
end

The result we get back is 6 for this one. If we follow the same formula of

ciphertext_byte xor guess xor result

We get 2 ^ 6 ^ 2, which is 6. So we we have decrypted another byte. Let’s use that to force our padding to three.

ciphertext[15] = (original_ct[15].ord ^ 6 ^ 3).chr
ciphertext[14] = (original_ct[14].ord ^ 6 ^ 3).chr
(0..255).each do |b|
    ciphertext[13] = b.chr
    begin
        decrypt(ciphertext)
        puts b
    rescue
        next
    end
end

The result is 27. 30 ^ 27 ^ 3 is yet again, 6. Which is what we expect since we expect 6 padding bytes with a value of 6.

For the sake of brevity, let’s skip ahead a bit. Let’s see what happens if we trick it in to thinking there are 7 padding bytes.

ciphertext[15] = (original_ct[15].ord ^ 6 ^ 7).chr
ciphertext[14] = (original_ct[14].ord ^ 6 ^ 7).chr
ciphertext[13] = (original_ct[13].ord ^ 6 ^ 7).chr
ciphertext[12] = (original_ct[12].ord ^ 6 ^ 7).chr
ciphertext[11] = (original_ct[11].ord ^ 6 ^ 7).chr
ciphertext[10] = (original_ct[10].ord ^ 6 ^ 7).chr
(0..255).each do |b|
    ciphertext[9] = b.chr
    begin
        decrypt(ciphertext)
        puts b
    rescue
        next
    end
end

The result is 198. 166 ^ 198 ^ 7 is 103. 103 on the ASCII table is “g”. Our plaintext string ends in a “g”. Let’s keep advancing.

ciphertext[10] = (original_ct[10].ord ^ 6 ^ 8).chr
ciphertext[9] = (original_ct[9].ord ^ 103 ^ 8).chr
# etc...

We get 198, and 160 ^ 198 ^ 8 is “n”. If we repeat this pattern, we can fully decrypt the block. Let’s automate this a bit now.

ciphertext.freeze
decrypt_data = ciphertext.dup
recovered = {}
(1..16).each do |i|
    position = 16-i
    (0..255).each do |guess|
        decrypt_data[position] = guess.chr
        begin
            decrypt(decrypt_data)
        rescue
            next # Bad padding.
        end
        recovered[position] = ciphertext[position].ord ^ guess ^ i
        (1..i).each do |j|
            z = 16 - j
            decrypt_data[z] = (ciphertext[z].ord ^ recovered[z] ^ (i+1)).chr
        end
        break
    end
end
pp recovered.sort.map { |k, v| v }.pack("c*")

The final output is:

for coding\x06\x06\x06\x06\x06\x06

The everything put together example of attacking padding is available on GitHub. You can run that in most online ruby REPLs, like repl.it.

The crucial thing about this is that the “decrypt” process never returns the decrypted data, it either raises an exception or returns “Data processed”. Yet we were still able to determine the contents.

A common example of this is encrypted data over insecure transports and home-grown transport protocols. Such an example might be two servers that need to communicate with each other securely. The owners of the servers are able to pre-share an AES key for data transmission, say with a configuration file of sorts, so they assume they don’t need to use HTTPS because they can use AES-CBC to communicate data with their preshared keys. If that encrypted data is intercepted, and the intercepter is able to re-submit that data to one of the servers with padding changed, they are now able to decrypt this data.

Aside: You really should just use TLS with a modern configuration of protocol and cipher suites.

The solution for this is to authenticate our cipher text, which is to say, make it tamper-proof. This is easier said than done.

Let’s clean up symmetric encryption a bit to make it less of an example.

def process_data(iv, data)
    cipher = OpenSSL::Cipher::AES.new(128, :CBC)
    cipher.padding = 0
    cipher.decrypt
    cipher.key = @aes_key
    cipher.iv = iv
    plaintext = cipher.update(data)
    last_octet = plaintext[-1].ord
    raise PaddingError if plaintext.length - last_octet < 0
    padding = plaintext[-last_octet..-1]
    is_padding_valid = padding.bytes.inject(0) { |a, b|
        a | (b ^ last_octet)
    }.zero?
    raise PaddingError unless is_padding_valid

    # Process data
    return true
end

There. We have a function that takes an independent initialization vector and the data, and does a little bit more error handling. It still has flaws mind you, regarding padding removal. There are also some short comings of our attack, such has handling the case where the amount of padding on the ciphertext really is one or decrypting multiple blocks. Both of those are currently left as an exercise.

The usual means of authenticating AES-CBC is with an HMAC using Encrypt-then-MAC (EtM) to ensure the integrity of the ciphertext. Let’s cleanup our code a bit and reduce the amount of assumptions we make. No more hard coded keys and IVs. We’ll go with in-memory values, for now.

The final cleaned up version of this is also available on GitHub. For brevity, here are the function definitions:

def encrypt_data(plaintext); # return is [ciphertext, random_iv]
def process_data(iv, data); #return is "true", or an exception is raised

HMAC is a symmetric signature, or a “keyed hash”. If we sign the contents of the cipher text, then validate the HMAC before attempting to decrypt the data, then we have reasonable assurance that the cipher text has not been changed.

Let’s update the encrypt_data function to include a MAC.

HASH_ALGORITHM = 'sha256'.freeze

def encrypt_data(plaintext)
    new_iv = OpenSSL::Random.random_bytes(16)
    cipher = OpenSSL::Cipher::AES.new(128, :CBC)
    cipher.encrypt
    cipher.key = @aes_key
    cipher.iv = new_iv
    ciphertext = cipher.update(plaintext) + cipher.final
    digest = OpenSSL::Digest.new(HASH_ALGORITHM)
    mac = OpenSSL::HMAC.digest(digest, @hmac_key, ciphertext)
    [mac.freeze, ciphertext.freeze, new_iv.freeze]
end

Our encrypt function now returns the MAC as well. Many uses of EtM simply prepend the MAC to the front of the cipher text. The MAC’s size will be consistent with the underlying algorithm. For example, HMAC-SHA256 will always produce a 256-bit length digest, or 32-bytes. When it comes time to decrypt the data, the HMAC is split off from the cipher text since the length is known.

The process_data can be updated like this:

HASH_ALGORITHM = 'sha256'.freeze

def process_data(iv, mac, data)
    raise MacError if mac.length != 32
    digest = OpenSSL::Digest.new(HASH_ALGORITHM)
    recomputed_mac = OpenSSL::HMAC.digest(digest, @hmac_key, data)
    is_mac_valid = 0
    (0...32).each do |index|
        is_mac_valid |= recomputed_mac[index].ord ^ mac[index].ord
    end
    raise MacError if is_mac_valid != 0

    # Continue normal decryption

Our attack on the padding no longer works. When we attempt to tweak the first block, the HMAC no longer matches the supplied value. As an attacker, we can’t feasibly re-compute the HMAC without the HMAC key, and trying to guess one that works is also not doable.

We have some simple authenticated data applied to AES-CBC now, and defeated our padding oracle attack.

Authenticated encryption is a bare minimum for properly encrypting data, it isn’t “bonus” security. This attack is not new, is have been known at least since Vaudenay described it in 2002. Yet application developers continue to use unauthenticated encryption. Part of that is because people have stated that this oracle attack can be mitigated by not revealing that there was a padding error during decryption and instead being generic about the failure. This was likely incorrect advice - the correct solution is to authenticate the data which mitigates the padding oracle attack quite well.

We’re not quite done yet. In a later post, we’ll look at some of the problems with authenticating data using HMAC or using a mode of AES that is already authenticated like AES-GCM.