Examining the details of public key pinning
I’ve been working on adding some features around HTTP Public Key Pinning to my FiddlerCert Fiddler extension.
Specifically, I added indicators next to each certificate if it was pinned by
either the Public-Key-Pins or Public-Key-Pins-Report-Only header as well as
display the SPKI hash.
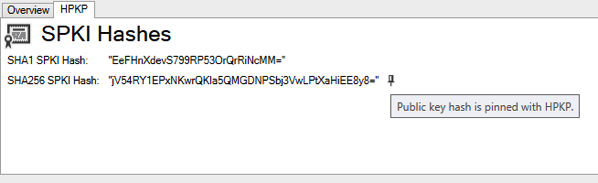
While implementing this, I learned quite a bit about what a pinned key is.
So, what is a pinned key? They are called a public key pin, but the pin is more than a hash of just the public key. You could for example, look at the public key of my domain:
04 35 D7 8F 8C 16 18 9D 1E 95 95 67 1C 39 D8 83
B3 32 1C 89 BA A3 56 78 8D C2 43 DB 20 4F 1D FA
80 93 6B 23 AF 1C 5A 59 F9 1B 74 A7 6F 62 38 97
A9 1B 29 2A 0F DA 40 B0 6F F9 6A 98 CE 45 48 48
2C
However if we were to take these bytes and hash them, it would not produce the same hash that OpenSSL does when following the recommended guidelines for producing a Public-Key-Pin hash.
The hash needs to include a little more information. For example, hashing just the public key doesn’t include certain other components, like what algorithm the key is, such as RSA or ECDSA. Other relevant information should be included as well, such as the public key exponent for RSA, or the identifier of the elliptic curve for ECDSA, or algorithm parameters.
Why do we need these extra values? Adam Langley has the details on his blog:
Also, we’re hashing the SubjectPublicKeyInfo not the public key bit string. The SPKI includes the type of the public key and some parameters along with the public key itself. This is important because just hashing the public key leaves one open to misinterpretation attacks. Consider a Diffie-Hellman public key: if one only hashes the public key, not the full SPKI, then an attacker can use the same public key but make the client interpret it in a different group. Likewise one could force an RSA key to be interpreted as a DSA key etc.
One tricky thing with hashing is that the data format must always be consistent. Since a hash operates on pure data and knows nothing about the structure of the data, the structure must be consistent and platform independent. Should the public key exponent be included before or after the public key? What endianness is the data? How is the data consistently represented?
For all of the grief it gives people, that’s what ASN.1 encoding is exactly for. What actually ends up getting hashed is a SubjectPublicKeyInfo (SPKI) portion of the X509 certificate. This includes all of the data that we need. In OpenSSL, it’s this part:
Subject Public Key Info:
Public Key Algorithm: id-ecPublicKey
Public-Key: (256 bit)
pub:
04:35:d7:8f:8c:16:18:9d:1e:95:95:67:1c:39:d8:
83:b3:32:1c:89:ba:a3:56:78:8d:c2:43:db:20:4f:
1d:fa:80:93:6b:23:af:1c:5a:59:f9:1b:74:a7:6f:
62:38:97:a9:1b:29:2a:0f:da:40:b0:6f:f9:6a:98:
ce:45:48:48:2c
ASN1 OID: prime256v1
NIST CURVE: P-256
In ASN.1 form, it looks like this.
30 59 30 13 06 07 2a 86 48 ce 3d 02 01 06 08 2a 86 48 ce 3d 03 01 07 03 42 00 04 35 d7 8f 8c 16 18 9d 1e 95 95 67 1c 39 d8 83 b3 32 1c 89 ba a3 56 78 8d c2 43 db 20 4f 1d fa 80 93 6b 23 af 1c 5a 59 f9 1b 74 a7 6f 62 38 97 a9 1b 29 2a 0f da 40 b0 6f f9 6a 98 ce 45 48 48 2c
The green portion should look familiar, it’s the public key. The rest of the bytes are part of the ASN.1 encoding.
ASN.1 Primer
ASN.1 is simple in concept, but difficult to write code for in a secure manner. ASN.1 consists of tags. Each tag consists of three things: the type of the tag (tag identifier), the length of the tag’s value, and the value of the tag. Tags can consist of other tags. Take this example:
06 07 2a 86 48 ce 3d 02 01
This is an OBJECT_IDENTIFIER. 0x06 is the identifier for an OBJECT_IDENTIFIER.
The next value is 7. The rest of the tag is the value, 2a 86 48 ce 3d 02 01 and
we see that it is exactly 7 bytes long, just as the length value said it was.
The data in an OBJECT_IDENTIFIER is a variable-length-quantity. This particular
OBJECT_IDENTIFIER’s value is an OID of 1.2.840.10045.2.1, which is the OID for
an ECC Public Key, or as we saw from OpenSSL’s output, id-ecPublicKey.
0x30, as the data starts with, is the tag identifier for a SEQUENCE. A SEQUENCE is a collection of other tags. The length value of a sequence is not the number of items in the sequence, but rather the total byte length of it’s contents. The only way to get the number of items in a sequence is to examine each of the tags in it and parse them out.
How the data in the ASN.1 data is stored is defined by the encoding rules. It can be DER, which is what is used with X509, or BER.
Breaking down the ASN.1 data, it looks like this:
SEQUENCE
SEQUENCE
OBJECT_IDENTIFIER 1.2.840.10045.2.1
OBJECT_IDENTIFIER 1.2.840.10045.3.1.7
BIT STRING 000435D78F8C16189D1E9595671C39D883B3321C89BAA356788DC243DB204F1DFA80936B23AF1C5A59F91B74A76F623897A91B292A0FDA40B06FF96A98CE4548482C
This is for an ECC public key. For an RSA public key, it would not have two OBJECT_IDENTIFIERs, but rather also include the public exponent.
FiddlerCert needed to do this, but backwards. Given a public key blob and the
parameters, convert it to ASN.1 data so it can be hashed. It was tempting to try
assembling the data myself, but I quickly realized this was very error prone.
Instead, I settled on using the CryptEncodeObject Win32 function with platform
invoke. This made it much simpler. All I had to do was construct a
CERT_PUBLIC_KEY_INFO structure that had all of the values and it happily
produced the ASN.1 data that was needed.
The implementation details of this are on GitHub in the CertificateHashBuilder class.